Thread Rating:

- Casino War is a relatively simple game as we’ve explained but you should understand the house edge for the various types of bets. All online casinos with have an advantage over their players (known as House Edge) as they will make a certain% overall.
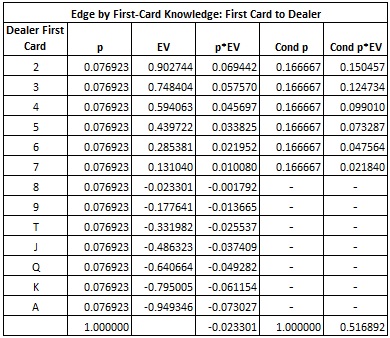
- Casino War is a proprietary casino table game based on the game of War.It is distributed by Shuffle Master, a division of Scientific Games. The game is one of the most easily understood casino card games, and is one of the only card games where players can beat the dealer more than 50% of the time.
The house edge is also known as the casino advantage. And it's something that exists on every table game, lotto, or slot in a casino online or on land. House edge tells you: How much each game pays.
dogmaticgamble
Casino House Edge
I have often heard the following about going to war in casino war:
'I'm often asked where the house edge lays in this game. Where the edge comes from is when there is a war you either win one unit or lose two. For example, if you originally bet $5 you have to double your bet, risking $10, to win only $5.'
I disagree entirely
In order to explain my analysis I need the following assumptions:
A) If the odds of winning increases for the player, then the player should always increase his/her bet.
B) if the player always wins ties, then the player has better odds then if the player never wins ties
C) If the player always wins ties, then the player has the advantage(this one is not needed but because its true my point is even more valid)
Analysis: WLOG let the following 5's represent 5 dollar chips...
NOTE: the actually numbers used is to simplify the explanation and does not actually matter...
you put down 5 5(ten dollars) on the table dealer risks 5 5 so 5 5 | 5 5
you claim that never surrendering is 5 5 5 5 | 5 5(20 you 10 dealer)...this is incorrect
Proof:
assume the player only has four 5 chips...and the bank only has 2(the bank never needs to touch more)
5 5 5 5 player 5 5 bank
so let a tie occur...
Case one: you always surrender(push bet once)
you put out 5 5 and take back 5 so now it is
5 5 5 player 5 5 5 bank
you then proceed to bet 5 5 5(last chips the player has left) you now have Q chance to win back 5 5 5 so risks are 5 5 5 | 5 5 5
NOTE: all chips are on the table for the player to win with Q chance(chance of winning where ties are a loss)
Case two: you always surrender and never push bet
you put out 5 5 and take back 5 so now it is
5 5 5 player 5 5 5 bank
you then proceed to bet 5 5 you now have Q chance to win back 5 5
you then proceed to bet 5 you now have Q chance to win back 5
NOTE: chance to leave with all the chips is now 1-(1-Q)^2
Case three: you dont surrender this time
you put out 5 5 and then put out 5 5 so now it is
5 5 5 5 of the players and 5 5 of the bank money before the original flip
you now have a P chance of winning
NOTE: all chips are on the table for the player to win with P chance(chance of winning where ties are a win)
Conclusions:
In both situations the player has all of their chips on the table at the conclusion and the bank has all of its chips on the table:
In case one the player has Q chance of leaving the casino with all the chips
In case two the player has P chance of leaving the casino with all the chips
by assumption B) the player has better odds of winning in case three then case one
by assumption A) the player therefore has better odds of winning in case three then case two
so the player has best odds of winning in case three(the dont surrender)
therefore you should NEVER surrender...
Error:
The reason the initial statement was incorrect is the moment you tie the bank has already won one of the 5 chips...so when you place out two more 5 chips you have put out three 5 5 5(one of original and two more) and the bank has MATCHED this...
because you now win ties(and win more if this happens) your odds have gone up so pushing your bet is not ignorant(assumption A) also because of assumption C you actually have over 50% chance to win your money
Analysis:
if you always play ties(the better play by above), your odds of winning are...
W=chance to win with no ties a bit less then 50%
E=chance to tie a small amount
J=chance to lose a bit less then 50%
J=W
NOTE: W+E(.5)=.5
then Probability that you win is...
P=W+E*(W+E*1.5)+0*J (you win 50% more if it ties twice)
P=W+E(W+1.5-3W)=W+E(1.5-2W)
W<.5 so 2W<1 so
P>W+E(.5)=.5
so odds are > 50 % chance to win
Why:
So why does the casino still play the game?
At least three big reasons...
players often dont want to do equal bets for the same reason that you originally said it was a bad idea. this gives the casino a bigger then 50% chance to win
players often come to the table to just send their last chips until they lose them(dont walk away)
Gamblers fallacy...players increase there bets as they win...this increases the odds of loses it all
As you can see if you play the same amount every time AND you ALWAYS go to war, you have >50% chance to win...but as a human who has seen a coin come up heads more then 10 times in a row. over 50% chance to win does not mean you will always make money
'I'm often asked where the house edge lays in this game. Where the edge comes from is when there is a war you either win one unit or lose two. For example, if you originally bet $5 you have to double your bet, risking $10, to win only $5.'
I disagree entirely
In order to explain my analysis I need the following assumptions:
A) If the odds of winning increases for the player, then the player should always increase his/her bet.
B) if the player always wins ties, then the player has better odds then if the player never wins ties
C) If the player always wins ties, then the player has the advantage(this one is not needed but because its true my point is even more valid)
Analysis: WLOG let the following 5's represent 5 dollar chips...
NOTE: the actually numbers used is to simplify the explanation and does not actually matter...
you put down 5 5(ten dollars) on the table dealer risks 5 5 so 5 5 | 5 5
you claim that never surrendering is 5 5 5 5 | 5 5(20 you 10 dealer)...this is incorrect
Proof:
assume the player only has four 5 chips...and the bank only has 2(the bank never needs to touch more)
5 5 5 5 player 5 5 bank
so let a tie occur...
Case one: you always surrender(push bet once)
you put out 5 5 and take back 5 so now it is
5 5 5 player 5 5 5 bank
you then proceed to bet 5 5 5(last chips the player has left) you now have Q chance to win back 5 5 5 so risks are 5 5 5 | 5 5 5
NOTE: all chips are on the table for the player to win with Q chance(chance of winning where ties are a loss)
Case two: you always surrender and never push bet
you put out 5 5 and take back 5 so now it is
5 5 5 player 5 5 5 bank
you then proceed to bet 5 5 you now have Q chance to win back 5 5
you then proceed to bet 5 you now have Q chance to win back 5
NOTE: chance to leave with all the chips is now 1-(1-Q)^2
Case three: you dont surrender this time
you put out 5 5 and then put out 5 5 so now it is
5 5 5 5 of the players and 5 5 of the bank money before the original flip
you now have a P chance of winning
NOTE: all chips are on the table for the player to win with P chance(chance of winning where ties are a win)
Conclusions:
In both situations the player has all of their chips on the table at the conclusion and the bank has all of its chips on the table:
In case one the player has Q chance of leaving the casino with all the chips
In case two the player has P chance of leaving the casino with all the chips
by assumption B) the player has better odds of winning in case three then case one
by assumption A) the player therefore has better odds of winning in case three then case two
so the player has best odds of winning in case three(the dont surrender)
therefore you should NEVER surrender...
Error:
The reason the initial statement was incorrect is the moment you tie the bank has already won one of the 5 chips...so when you place out two more 5 chips you have put out three 5 5 5(one of original and two more) and the bank has MATCHED this...
because you now win ties(and win more if this happens) your odds have gone up so pushing your bet is not ignorant(assumption A) also because of assumption C you actually have over 50% chance to win your money
Analysis:
if you always play ties(the better play by above), your odds of winning are...
W=chance to win with no ties a bit less then 50%
E=chance to tie a small amount
J=chance to lose a bit less then 50%
J=W
NOTE: W+E(.5)=.5
then Probability that you win is...
P=W+E*(W+E*1.5)+0*J (you win 50% more if it ties twice)
P=W+E(W+1.5-3W)=W+E(1.5-2W)
W<.5 so 2W<1 so
P>W+E(.5)=.5
so odds are > 50 % chance to win
Why:
So why does the casino still play the game?
At least three big reasons...
players often dont want to do equal bets for the same reason that you originally said it was a bad idea. this gives the casino a bigger then 50% chance to win
players often come to the table to just send their last chips until they lose them(dont walk away)
Gamblers fallacy...players increase there bets as they win...this increases the odds of loses it all
As you can see if you play the same amount every time AND you ALWAYS go to war, you have >50% chance to win...but as a human who has seen a coin come up heads more then 10 times in a row. over 50% chance to win does not mean you will always make money
blueleaf
A complete wrong idea, no betting system works, cant stop laugh.
SM777
Well, those brain cells I'll never get back.
apples
I miss Casino War. I played it once at O'sheas. I think it was O'sheas that long ago. I got beat really bad. I think the best is Griswold playing that game at the klondike. He lost 40 bux pretty fast!
The Edge Casino
gamerfreak
I miss Casino War. I played it once at O'sheas.
It's the only table game I can convince my girlfriend to 'learn' so I give it a 10/10.